Algo do que tiña gana fai moito tempo era escribir un pequeno artigo acerca da escala temperada, sobre todo dende que escoitei o capítulo Disonancia de Catástrofe Ultravioleta.
O estudio das diferentes escalas é algo (ou era, polo menos nos meus tempos) que se estudaba en plan memorístico mesturado coa teoría da Linguaxe Musical (aka solfeo). E a verdade é que a un neno toda esa información metida aí, con calzador, non lle resulta de moito interés.
Pero si que é interesante o proceso de resumir e explicar a orixe da escala musical que se emprega hoxe no mundo occidentalizado. Máis que nada como exercicio para aclarar conceptos e, xa de paso, que quede por escrito (que a memoria é fráxil).
Así que comecemos xa.
A serie harmónica. #
Chámase serie harmónica á sucesión de sons que se forman a partir dun son base ou frecuencia fundamental, mediante o proceso de ir multiplicando a súa frecuencia por 2, 3, 4, etc…
Nun instrumento musical, ou en calquera cousa que vibre, a frecuencia é inversamente proporcional á lonxitude da corda vibrante, ou do tubo resonante (cando o que vibra é o aire). Deste xeito, podemos xerar unha serie harmónica partindo dunha corda que vibra simplemente acurtando a súa lonxitude ó dividila por 2, logo por 3, por 4, etc…
| Harmónico | Frecuencia | Comentario |
|---|---|---|
| 1º | F | Frecuencia base ou fundamental. |
| 2º | 2·F | Primeira oitava. |
| 3º | 3·F | Quinta respecto do 2º harmónico. |
| 4º | 4·F | Segunda oitava. |
| 5º | 5·F | Terceira maior respecto do 4º harmónico. |
| 6º | 6·F | Terceira menor respecto do 5º harmónico. Oitava do 3º armónico. |
| 7º | 7·F | Non se emprega para construir intervalos. |
| 8º | 8·F | Terceira oitava. |
| 9º | 9·F | Segunda maior respecto do 8º harmónico. |
| 10º | 10·F | Segunda maior respecto do 9º harmónico. |
| 11º | 11·F | Non se emprega para construir intervalos. |
| 12º | 12·F | Oitava do 6º harmónico. |
| 13º | 13·F | Non se emprega para construir intervalos. |
| 14º | 14·F | Ainda que é unha oitava do 7º harmónico, ó non ser este útil para os intervalos, tampouco o é a súa oitava. |
| 15º | 15·F | Quinta xusta respecto do 10º harmónico. |
| 16º | 16·F | Cuarta oitava. Segunda menor respecto do 15º harmónico. |
— Uffff… pero, ¿que é todo isto que pon nesta táboa?
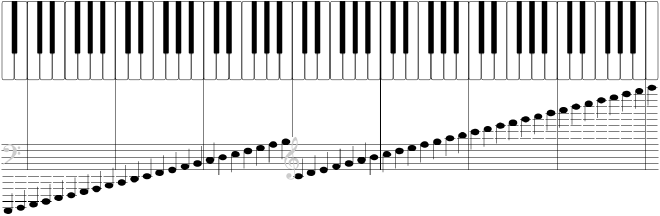
Non nos botemos as mans á cabeza e vaiamos por partes. O primeiro que debemos saber é que é iso de unha “oitava”. Unha oitava non é máis ca unha nota que está a unha frecuencia xusto o dobre de outra. O que teñen de característico as oitavas é que as percibimos coma se fosen o mesmo son, ainda que sexan efectivamente máis agudas ou máis graves. Se tomamos o exemplo dun piano (que resulta moi útil para explicar todo isto), veremos que as súas teclas ordénanse segundo unha disposición característica pola que se forman grupos de teclas que se repiten ó longo de todo o teclado. Se collemos dúas teclas que ocupen a mesma posición dentro de dous grupos consecutivos, esas dúas teclas reproducirán a mesma nota, terán o mesmo son, só que un máis agudo có outro.
Unha escala musical consiste nunha serie de sons de diferente frecuencia, ordenados de menor a maior, e limitados por unha oitava. É dicir, ó construir unha escala quedámonos únicamente cos sons que quedan entre unha nota e a súa oitava máis próxima, porque logo non fai falla máis que repetir as oitavas de cada un destes sons sucesivamente.
Chámase intervalo á distancia entre dúas notas musicais. Así, a distancia entre dúas notas consecutivas é un intervalo de segunda, a distancia entre a primeira e a última nota dun grupo de tres consecutivas é un intervalo de terceira, etc… Logo os intervalos poden ser menores, xustos ou maiores, pero diso xa falaremos noutra ocasión (ainda que non teñades moitas esperanzas).
Como construímos os sons intermedios da escala, se todos os que obtivemos na serie harmónica están claramente fóra da oitava? Si, é certo. O segundo harmónico é a oitava do primeiro (ten xustamente o dobre da súa frecuencia), e a partir de aí as frecuencias seguen aumentando, así que non temos ningún valor que estea entre o primeiro (a fundamental) e o segundo (a primeira oitava).
O segredo está en que o interesante da serie harmónica non son os valores das frecuencias que produce, senón na relación que existe entre elas. Imos escoitar un exemplo de escala harmónica na que tomamos como base a frecuencia de 110 Hz:
6º harmónico a 660 Hz 7º harmónico a 770 Hz 8º harmónico a 880 Hz 10º harmónico a 1100 Hz 11º harmónico a 1210 Hz
¿Que tal andamos de oído? #
Veña, vai. De seguro que reproducistes os sons da escala anterior. Que tal soaron? Ben? Non vos rechiou ningún?
Imos revisalos un pouco.
Se reproducimos dende o primeiro harmónico ata o sexto, todo parece encaixar. Os sons soan “harmónicamente”, parece que ningún desafina e entre todos forman unha progresión que nos resulta agradable ó oído. A nosa tradición musical tamén inflúe en que a nosa percepción sexa esa, ollo. Toda a nosa herdanza musical condiciona os nosos gustos e inflúe no que nos parece harmónico e o que nos resulta disonante.
Pero chegamos ó sétimo harmónico e… hmmmm. Non. Definitivamente ese son non pega moito cos anteriores, non pensades?. Semella coma se se rompese a progresión que soaba tan ben e esa nota estea desafinada respecto das demáis. Esa é a razón pola que na primeira táboa se indicaba que o sétimo harmónico non se emprega para construír intervalos.
Aquí tedes a secuencia 1º-2º-3º-4º-5º-6º-7º nun único arquivo:
Veña, imos reproducir de novo a nosa escala harmónica, pero desta vez saltámonos o sétimo harmónico polo mal que soa e seguimos ata o onceavo, co que a secuencia de harmónicos queda en 1º-2º-3º-4º-5º-6º-8º-9º-10º-11º:
Que tal agora? Mellor? Algo si que mellorou, non?
Algún de vós dudará no noveno harmónico e quedará coa sensación de que nin desentoa nin queda mal de todo. Se probásemos a quita-lo noveno a escala poderíanos soar case mellor, pero iso non quere dicir que o noveno sexa dos que “rechíen”, así que conservámolo. Porén, o undécimo definitivamente soa mal e por iso na primeira táboa tamén figura a indicación de que non é útil para construír intervalos.
Se continuamos cos seguintes sons, veremos (mellor dito, escoitaremos) que o décimo terceiro harmónico tamén é dos desagradables, e co décimo cuarto ocorre o mesmo (lembremos que o décimo cuarto harmónico non é máis ca unha oitava -o dobre- do sétimo harmónico, e polo tanto é igual de “feo”).
Así que da nosa escala harmónica válennos tódolos sonidos, excepto o 7º, 11º, 13º e 14º. O 9º deixámolo a gusto do consumidor e eu decidín conservalo, polo que nos queda a secuencia 1º-2º-3º-4º-5º-6º-8º-9º-10º-12º-15º-16º:
Que comece a festa! #
Lembrades o que dicíamos da oitava? Dúas notas que estean a distancia dunha oitava soan de xeito semellante, só que unha máis aguda cá outra (vou ser moi pesado con isto, tedes que desculparme). Pois ben, para construír unha escala non temos que usar frecuencias tan dispares. Basta con que nos quedemos con frecuencias que estean entre a fundamental e a primeira oitava.
Pero como comentamos tamén antes, resulta que tódolos nosos harmónicos están por riba da primeira oitava, así que o que acabamos de dicir non parece que sirva de moito. Podemos facer unha cousa: baixar os harmónicos unha, dúas, tres oitavas, ou as que precisemos, ata que queden dentro da primeira.
Resumindo, imos colle-las frecuencias da táboa dos nosos harmónicos “útiles”, e imos dividir-la súa frecuencia por dous para baixalos unha oitava; e se a frecuencia resultante segue a estar moi alonxada da frecuencia fundamental, volverémolos a dividir por dous tantas veces como sexa necesario. Deste xeito estamos baixando as notas dos harmónicos as oitavas que sexan necesarias para que queden na mesma oitava que a frecuencia fundamental que orixinou a serie harmónica, pero como só os estamos cambiando de oitava, en realidade seguen a ser a mesma nota. Para baixar unha oitava simplemente dividiremos a frecuencia entre dous; para baixar dúas oitavas dividiremos entre dous, dúas veces (isto é, entre catro); para baixar tres oitavas dividiremos entre oito, e así cantas veces precisemos.
Pois logo, e cos nosos harmónicos “útiles” (a secuencia 1º-2º-3º-4º-5º-6º-8º-9º-10º-12º-15º-16º), quedaríanos:
| Harmónico | Frecuencia | Frecuencia corrixida |
|---|---|---|
| 1º | 110 Hz | 110 Hz |
| 2º | 220 Hz | 220 : 2 = 110 Hz (baixamos unha oitava) |
| 3º | 330 Hz | 330 : 2 = 165 Hz (baixamos unha oitava) |
| 4º | 440 Hz | 440 : 4 = 110 Hz (baixamos dúas oitavas) |
| 5º | 550 Hz | 550 : 4 =137,5 Hz (baixamos dúas oitavas) |
| 6º | 660 Hz | 660 : 4 = 165 Hz (baixamos dúas oitavas) |
| 8º | 880 Hz | 880 : 8 = 110 Hz (baixamos tres oitavas) |
| 9º | 990 Hz | 990 : 8 = 123,75 (baixamos tres oitavas) |
| 10º | 1100 Hz | 1100 : 8 = 137,5 Hz (baixamos tres oitavas) |
| 12º | 1320 Hz | 1320 : 8 = 165 Hz (baixamos tres oitavas) |
| 15º | 1650 Hz | 1650 : 8 = 206,25 Hz (baixamos tres oitavas) |
| 16º | 1760 Hz | 1760 : 16 = 110 Hz (baixamos catro oitavas) |
Como se pode apreciar, agora moitas das frecuencias dos harmónicos repítense, polo que volvemos a quedar só con aquelas que non estean duplicadas:
| Harmónico | Frecuencia | Frecuencia corrixida |
|---|---|---|
| 1º | 110 Hz | 110 Hz |
| 3º | 330 Hz | 330 : 2 = 165 Hz (baixamos unha oitava) |
| 5º | 550 Hz | 550 : 4 =137,5 Hz (baixamos dúas oitavas) |
| 9º | 990 Hz | 990 : 8 = 123,75 (baixamos tres oitavas) |
| 15º | 1650 Hz | 1650 : 8 = 206,25 Hz (baixamos tres oitavas) |
Estes serían os sons dos harmónicos reducidos á primeira oitava:
Agora imos ordenalos:
| Harmónico | Frecuencia | Frecuencia corrixida |
|---|---|---|
| 1º | 110 Hz | 110 Hz |
| 9º | 990 Hz | 990 : 8 = 110 * 9/8 = 123,75 Hz |
| 5º | 550 Hz | 550 : 4 = 110 * 5/4=137,5 Hz |
| 3º | 330 Hz | 330 : 2 = 110 * 3/2= 165 Hz |
| 15º | 1650 Hz | 1650 : 8 = 110 * 15/8= 206,25 Hz |
E, que tal se escoitaría esta secuencia ascendente? Imos aló:
Vaia! Isto vai collendo corpo. De seguro que cantarexastes o “Do-Re-Mi” nas tres primeiras notas. Ainda que a nota fundamental que escollemos, a de 110 Hz, non é un Do, a secuencia que acabamos de construír soa similar. Isto é así porque son as tres primeiras notas cunha escala maior e os seus intervalos (a “distancia” sonora que hai entre unha nota e outra) son os mesmos que os que ten a escala que coñece todo o mundo, que é a escala maior de Do.
Se non dades demasiada vergoña cantando, e tentades segui-la secuencia cantarexando o “Do-Re-Mi…” (pero insisto! non é un Do-Re-Mi real) notaredes que lle faltan as notas que deberan ocupar o cuarto lugar (Fa) e o sexto lugar (La). E para pecha-la cancionciña, o seu sería rematar coa oitava (o Do máis agudo).
Para que poidades comprobalo, imos repetir a secuencia anterior, pero deixando os silencios das notas que faltan e pechando coa oitava:
Completastes o ocos que faltan? Saen sós, non si? De novo, é a tradición musical a que nos condiciona.
A importancia das proporcións #
Que é o que fai que os sons que xeramos soen máis ou menos ben? Ó fin e ó cabo, non fixemos máis que multiplicar e dividir unha fecuencia calquera.
Pois ben, ese é o segredo: as proporcións. Na táboa de harmónicos corrixidos aparecen as proporcións existentes entre a frecuencia fundamental e cada unha das demáis notas coas que fomos construíndo a nosa “protoescala”, e que podedes ver na seguinte táboa:
| Nota ou grado | Proporción entre frecuencias | Denominación |
|---|---|---|
| 1º | 1:1 | Tónica |
| 2º | 9:8 | Supertónica |
| 3º | 5:4 | Mediante |
| 5º | 3:2 | Dominante |
| 7º | 15:8 | Subtónica ou sensible |
Nesta nova clasificación, deixamos de chamar ás notas polo seu harmónico, e tan só as volvemos numerar en orden ascendente. Deixamos baleiro os lugares cuarto e sexto, porque xa vimos que aí faltan notas que polo de agora non sabemos como van aparecer. Pero o importante é que nos fixemos en que unhas simples proporcións de números enteiros son as que controlan o cotarro, e iso era precisamente o que embelecaba ós antigos gregos: a música emanaba da natureza, facendo que unhas simples razóns matemáticas creasen sons harmónicos. Creando beleza.
Completamente harmónicos? Non! Unha pequena aldea gala resístese a… Ai, non, perdoade, que isto non iba aquí. Direivos que uns séculos máis tarde, os músicos quedaron fartos de tanta tontería de número enteiros e adoptaron unha escala que se olvida completamente dos números enteiros (salvo para a oitava). Pero non adiantemos acontecementos.
Volvamos ás nosas proporcións.
Completando a nosa protoescala… #
Deixáramos a nosa escala sen rematar. Quedábannos dous ocos nas posicións cuarta e sexta, lembrades? Pois imos completalos.
A cuarta nota, ou cuarto grado da nosa escala, conséguese mediante o intervalo de quinta, só que no canto de subir o que facemos é baixar.
Dito doutro xeito, se na nosa protoescala conseguimos a quinta nota multiplicando a frecuencia fundamental pola relación 3/2, o que faremos agora será dividir a frecuencia fundamental por 3/2, que ven sendo o mesmo que multiplicar pola razón inversa 2/3.
Si, si, xa sei que vos decatastes. Se multiplicamo-la frecuencia fundamental por 2/3, obteremos unha frecuencia menor, e polo tanto fóra da nosa oitava, arredemo! Pero iso arranxámolo fácilmente: multiplicamos por dous a frecuencia resultante para volver a metela dentro da nosa oitava. Igual que antes tivemos que dividir por dous para “corrixir” as frecuencias dos harmónicos e que non fosen tan altas, agora o que facemos é unha corrección semellante, pero multiplicando no canto de dividir.
Así e logo, a nosa cuarta nota obterémola multiplicando por 2/3 e logo multiplicando outra vez por 2, co que a relación total será de 4/3 respecto da frecuencia fundamental ou tónica. Como podedes ver, estamos outra vez ante unha relación de números enteiros sencillos. Que máquinas eran estes gregos…
A nosa cuarta nota, ou cuarto grado da escala, será polo tanto de 110 · 4/3 = 146,666… Hz, e soaría así:
E que pasa coa nota da sexta posición? Pois ben, a sexta posición pódese calcular tomando unha quinta dende a segunda nota. Ou o que ven sendo o mesmo: a distancia entre a sexta nota e a segunda ten que ser a mesma que hai entre a quinta nota e a primeira, o que se coñece coma intervalo de quinta.
Con isto, a frecuencia da nosa sexta nota tería que ser a correspondente á segunda nota multiplicada pola razón de quinta, que é 3/2. Como á súa vez a segunda nota ten unha frecuencia que é 9/8 respecto da fundamental, temos que a frecuencia da sexta nota ten que ser de (3/2)·(9/8)=27/16.
Visto todo o anterior, é doado calcular que a sexta nota deberá ter unha frecuencia de 110 · 27/16 = 185,625 Hz, e soará tal que así:
Como queda a nosa escala? Imos comprobalo:
| Nota ou grado | Proporción entre frecuencias | Frecuencia | Denominación |
|---|---|---|---|
| 1º | 1:1 | 110 Hz | Tónica |
| 2º | 9:8 | 123,75 Hz | Supertónica |
| 3º | 5:4 | 137,5 Hz | Modal ou mediante |
| 4º | 4:3 | 146,666… Hz | Subdominante |
| 5º | 3:2 | 165 Hz | Dominante |
| 6º | 27:16 | 185,625 Hz | Superdominante |
| 7º | 15:8 | 206,25 Hz | Subtónica ou sensible |
| 1º (Oitava) | 2:1 | 220 Hz | Tónica (oitava) |
Escala diatónica completa
Veña, que estades coma tolos por escoita-la escala completa. Aquí a tedes:
Xenial! Somos uns monstruos! Construímos unha escala musical a partir da nada! Ben, pois non nos poñamos estupendos, porque isto non fixo máis que comezar.
Son iguais tódolos intervalos da nosa escala? #
Imos fixarnos un pouco máis na nosa escala. Están tódalas notas igual de “separadas” entre si? Hai algunhas que estean máis “xuntas”?
Comparemos a relación de frecuencias que hai entre cada par de notas:
| Nota ou grado | Proporción entre frecuencias respecto da tónica | Proporción entre frecuencias respecto da nota anterior |
|---|---|---|
| 1º | 1:1 | |
| 2º | 9:8 | 9/8 : 1 = 9/8 |
| 3º | 5:4 | 5/4 : 9/8 = 10/9 |
| 4º | 4:3 | 4/3 : 5/4 = 16/15 |
| 5º | 3:2 | 3/2 : 4/3 = 9/8 |
| 6º | 27:16 | 27/16 : 3/2 = 9/8 |
| 7º | 15:8 | 15/8 : 27/16 = 10/9 |
| 1º (Oitava) | 2:1 | 2/1 : 15/18 = 16/15 |
| Relación de frecuencias entre grados da escala |
Como podedes ver, as distancias entre notas máis grandes son dunha relación de 9:8, mentres que as máis pequenas son de 16:15. A distancia ou relación de 9:8 é á que lle chamaremos un ton, mentres que á distancia ou relación de 16:15 chamarémoslle semitón.
Comezan os problemas #
Así e todo, vemos que entre a segunda e a terceira nota da nosa escala hai unha distancia de 10:9 que, se ben é semellante á de 9:8, non é exactamente a mesma. Ocorre o mesmo entre a sexta e a sétima.
Esta pequena diferencia fai que se aplicamos a distancia do semitón dúas veces, a relación que obtemos non é exactamente a do ton. Veámolo con detalle:
Subir un semitón corresponde a multiplica-la frecuencia pola relación 16:15 que vimos antes. Polo tanto, subir dous semitóns equivale a aplicar esa relación dúas veces e o factor polo que estaremos a multiplicar a frecuencia será de:
(16:15)2 = 256:225 = 1,137777…
Pero se en troques de subir dous semitóns decidimos subir un ton, é dicir, a relación de 9:8, resulta que o factor polo que multiplicamos é neste caso:
9:8 = 1,125 que obviamente non é o mesmo que 1,137777…
Outro efecto da non correspondencia entre o semitón como metade exacta dun ton, é que se temos dúas notas separadas por un ton, a nota intermedia entre elas será diferente en función de se a obtemos subindo un semitón dente a nota inferior ou de se a obtemos baixando un semitón dende a nota superior.
Esta desigualdade entre as distancias das notas da escala dase en calquera sistema de afinación que empregue razóns de números enteiros, e foi unha pequena pedra no zapato que estivo incordiando durante moitos séculos.
Hai máis métodos para construír escalas? #
Resposta curta: si.
O método que vimos, construíndo unha escala empregando os sons da serie harmónica e reducindo ou aumentando as súas frecuencias para poñelos todos na mesma oitava, non é o único xeito de construír unha escala. De feito, máis ca unha alternativa foi unha necesidade a procura doutras escalas que eliminaran ou polo menos atenuaran os problemas xerados polo feito de que as distancias entre as notas non sexan iguais cando utilizamos as relacións que aparecen na escala harmónica.
SPOILER: Hai construccións de escalas diferentes, e se comparásemos os seus sons veríamos que están “desafinadas” unhas respecto das outras. Pero todas soan ben, non vos preocupedes.
Non hai ningún método que iguale os semitóns (usando números enteiros, enténdese). As diferentes solucións que se foron adoptando ó longo do tempo simplemente redistribuían, con maior ou menor acerto, esa desigualdade entre os diferentes semitóns da escala.
Por exemplo, para arranxar ese intervalo de 10:9 que nos aparecía na escala que construímos antes, poderíamos calcular a terceira nota para que gardase unha relación de 9:8 respecto da segunda, pero entón a distancia entre a cuarta e a terceira xa non sería de 16:15.
A afinación pitagórica #
Os antigos gregos, e Pitágoras entre eles, eran un estudosos da teoría musical e das relacións entre os intervalos. Pódese dicir que o sistema musical occidental moderno ten as súas orixes nas escalas gregas, e segundo esta xente existían tres intervalos principais que respondían a unha relación de números enteiros:
| Intervalo | Relación | Significado |
|---|---|---|
| Oitava | 2:1 | É a distancia sonora entre os sons producidos por dúas cordas, onde a lonxitude dunha é o dobre da outra. |
| Quinta | 3:2 | É a distancia sonora entre os sons producidos por dúas cordas, cuxa relación de lonxitudes é de 3:2. |
| Cuarta | 4:3 | É a distancia sonora entre os sons producidos por dúas cordas, cuxa relación de lonxitudes é de 4:3. |
Destes tres intervalos, o de oitava realmente non aportaba musicalidade, porque non fai máis que subir e baixar oitavas, pero en realidade a nota segue a ser a mesma (si, son un pesado). O importante de verdade era o intervalo de quinta, mentres que o de cuarta non era máis que un de quinta “marcha atrás”, como xa vimos antes.
Estas proporcións xa nos soan, porque aparecían na progresión harmónica que estivemos a ver con anterioridade. Que teñen de importante estes intervalos? Pois básicamente, que lle soaban ben aos gregos (ou mellor dito, lles soarían ben a calquera). E fixádemos se lles soaban ben, que seguen dominando a música actual (ainda que os cambiamos un pouco). Ademáis de soar ben, as relacións entre eles estaban definidas por números enteiros e oes, iso á xente ilustrada coma os filósofos e matemáticos gregos gustáballe. Había algo guai en que a Natureza fose tan sabia de poder facer música cos números.
E como soan eses intervalos? Pos imos escoitalos.
A nosa nota base será agora un La 440 Hz, que corresponde cun La4. O do 4 non vai polo de 440, senón porque ás notas asígnaselles un número que indica en qué oitava están.
Para entendérmonos, se agrupamos as teclas dun piano por oitavas, o primeiro grupo de Do a Si sería a primeira oitava, e esas notas pasarían a chamarse Do1..Si1, co segundo grupo teríamos Do2..Si2, e así ata percorrer todo o teclado (quedarían algunhas notas soltas tanto á esquerda como á dereita, sen completar-la súa correspondente oitava).
Cada vez que cambiamos de oitava, o que temos son as mesmas notas que na oitava anterior, pero cuxa frecuencia é o dobre. É por iso polo que dous La de diferentes oitavas nos soan igual, aínda que un sexa máis grave e outro máis agudo. Lembrade isto, porque logo será necesario empregalo (xa me ocupo eu de machacárvolo).
Pois ben, o La da cuarta oitava é o La4, e é a nota que soa a 440 Hz. Isto implica que as frecuencias dos intervalos de cuarta, quinta e oitava serán os seguintes:
| Intervalo | Frecuencia fundamental | Relación | Frecuencia do intervalo |
|---|---|---|---|
| Tónica | 440 Hz | ||
| Cuarta | 440 Hz | 4:3 | 586,666… Hz |
| Quinta | 440 Hz | 3:2 | 660 Hz |
| Oitava | 440 Hz | 2:1 | 880 Hz |
E aquí temos os sons correspondentes:
Que significa iso de “Tónica”? Cando falamos da nota tónica referímonos á nota base da escala, é dicir, á nota a partir da que se forman tódalas demáis. Collemos o noso La4 como nota tónica, ou nota base, e a partir del calculamos as frecuencias dos intervalos de cuarta, quinta e oitava.
A nota resultante do intervalo de cuarta sería a cuarta nota da escala formada a partir do noso La4. Do mesmo xeito, a nota resultante do intervalo de quinta sería a quinta nota da escala formada a partir dese mesmo La4.
E a nota resultante do intervalo de oitava sería a oitava nota da nosa escala, pero como as escalas teñen sete notas (Do-Re-Mi-Fa-Sol-La-Si si comenzamos por un Do, o La-Si-Do-Re-Mi-Fa-Sol si comenzamos polo La), esta oitava nota non é maís ca a tónica da seguinte oitava. É dicir, que sería outro La, pero máis agudo: un La5.
Pois ben, ca nota tónica, a cuarta e a quinta dunha escala xa podemos construírnos unha liña básica de acompañamento que encaixaría con moitísimas composicións musicais. Non tedes máis que probar a reproducir os sons anteriores, por exemplo, nesta secuencia: Tónica-Cuarta-Quinta-Cuarta-Tónica… e así sucesivamente.
Veña, vai, xa sei que entonades moi mal, así que póñovolo eu:
E non estou a esaxerar: moitas, moitísimas cancións actuais empregan unha serie de acordes coa progresión I-IV-V. Pode cambiar a tonalidade, pero non a progresión.
Se vos pica a curiosidade e ledes un pouco máis sobre harmonía (cousa que non ides atopar aquí), comprenderedes que dentro dunha escala hai notas que lle dan a estrutura, é dicir, onde reside a forza da escala, e outras onde están os detalles, o sentimento. Ás notas que estruturan a escala chámaselles grados tonais, e ás notas que lle dan expresión e sentimento chamámoslles grados modais. Todo isto dito así simple e rápidamente. Que me perdoen os músicos que se sintan ofendidos, pero para ofenderse xa está Twitter.
Os nosos intervalos de cuarta e quinta forman a estrutura da nosa escala porque xunto coa tónica, forman os tres grados máis importantes da escala:
- Tónica, ou grado I
- Subdominante, cuarta, ou grado IV
- Dominante, quinta, ou grado V
Polo de agora, a nosa escala pitagórica segue a respetar as mesmas proporcións que xa vimos antes cando construímos a escala diatónica. E estaredes a preguntarvos que ocorre coas demáis notas da escala. Tamén xurden de xeito natural como relacións de enteiros? Pois si. Imos velos:
Ó señor Pitágoras chistáballe o intervalo de quinta, como bo roqueiro. Así que lle deu por estuda-las notas que saían aplicando o intervalo de quinta sucesivamente. Nós non íamos ser menos, así que poñámonos mans á obra:
| Intervalo | Frecuencia de partida | Relación | Frecuencia da quinta |
|---|---|---|---|
| 1ª Quinta | 440 Hz | 3:2 | 660 Hz |
| 2ª Quinta | 660 Hz | 3:2 | 990 Hz |
| 3ª Quinta | 990 Hz | 3:2 | 1485 Hz |
| 4ª Quinta | 1485 Hz | 3:2 | 2227,5 Hz |
| 5ª Quinta | 2227,5 Hz | 3:2 | 3341,25 Hz |
| 6ª Quinta | 3341,25 Hz | 3:2 | 5011,875 Hz |
| 7ª Quinta | 5011,875 Hz | 3:2 | 7517,8125 Hz |
| 8ª Quinta | 7517,8125 Hz | 3:2 | 11276,71875 Hz |
| 9ª Quinta | 11276,71875 Hz | 3:2 | 16915,078125 Hz |
| 10ª Quinta | 16915,078125 Hz | 3:2 | 25372,6171875 Hz |
| 11ª Quinta | 25372,6171875 Hz | 3:2 | 38058,92578125 Hz |
| 12ª Quinta | 38058,92578125 Hz | 3:2 | 57088,388671875 Hz |
Agora fixémonos nas frecuencias que nos saíron. Partindo da nosa frecuencia inicial de 440 Hz chegamos a máis de 57 KHz. A frecuencia máxima audible para un ser humano (e xove) é duns 20 KHz, así que nos pasamos tres pobos.
Supoño que vos estaredes a preguntar por que paramos na décimo segunda quinta. Tede paciencia.
A Quinta do Lobo #
Agora é o momento de lembrar o que dixemos sobre as oitavas (non sei se volo comentei antes X-D): cando pasamos da oitava, as notas que temos non son máis ca as mesmas notas, pero con frecuencia dobre. Se pasamos á seguinte oitava, dobramos a frecuencia; se subimos outra oitava máis, as frecuencias serán catro veces as iniciais; outra oitava máis e xa teríamos as frecuencias multiplicadas por 8, e así sucesivamente.
Onde queremos chegar? Pois que claramente, se na táboa anterior a nosa frecuencia inicial era de 440 Hz, a súa oitava será de 880 Hz e polo tanto calquera nota superior a 2 x 440 = 880 Hz estará nunha oitava diferente á de partida, calquera nota superior a 2 x 880 = 1760 Hz estará dúas oitavas máis arriba, etc…
O que toca facer a continuación, por se non o intuíades, é corrixi-la táboa anterior para acomoda-las frecuencias da cadea de quintas a notas que estén todas na mesma oitava. Para iso imos ir dividindo por 2 as frecuencias que calculamos, ata obter valores que estén entre 440 e 880 (que son os límites da nosa oitava inicial).
| Intervalo | Frecuencia sen corrixir | Corrección | Frecuencia corrixida |
|---|---|---|---|
| 1ª Quinta | 660 Hz | Non | 660 Hz |
| 2ª Quinta | 990 Hz | :2 | 495 Hz |
| 3ª Quinta | 1485 Hz | :2 | 742,5 Hz |
| 4ª Quinta | 2227,5 Hz | :4 | 556,875 Hz |
| 5ª Quinta | 3341,25 Hz | :4 | 835,3125 Hz |
| 6ª Quinta | 5011,875 Hz | :8 | 626,484375 Hz |
| 7ª Quinta | 7517,8125 Hz | :16 | 469,86328125 Hz |
| 8ª Quinta | 11276,71875 Hz | :16 | 704,794921875 Hz |
| 9ª Quinta | 16915,078125 Hz | :32 | 528,596191406 Hz |
| 10ª Quinta | 25372,6171875 Hz | :32 | 792,894287109 Hz |
| 11ª Quinta | 38058,92578125 Hz | :64 | 594,670715332 Hz |
| 12ª Quinta | 57088,388671875 Hz | :64 | 446,003036499 Hz |
Si, adiviñástelo. A razón de ter parado na décimo segunda quinta é que cando corriximos a frecuencia para baixala ata a oitava de partida, sáenos unha frecuencia que é moi semellante á frecuencia de base, o noso La4 a 440 Hz. E aquí é onde os gregos se quedaron chafados: sae unha frecuencia semellante, pero non igual.
Pero, por que esta diferenza? Non se supón que a Natureza era sabia e que a música emanaba de xeito natural dos números enteiros? Ben, pois parece que non de todo.
Comparemos o resultado de aplicar sete oitavas ou doce quintas á mesma nota de partida:
| Frecuencia da tónica | Intervalos aplicados | Relación | Frecuencia resultante |
|---|---|---|---|
| 440 Hz | 7 octavas | 27 : 1 | 56320 Hz |
| 440 Hz | 12 quintas | (3/2)12 : 1 | 57088,388671875 Hz |
Aiiiii… o balón foise ó largueiro. Resulta que non, que a Natureza non é tan sabia. A nota que sae se aplicamos doce quintas consecutivas NON corresponde coa séptima oitava.
A ese décimo primeiro intervalo de quinta chámaselle a quinta do lobo, por esa lixeira disonancia que facía que non coincidise exactamente coa tónica, e á diferenza entre amba-las dúas notas chámaselle coma pitagórica. Esta disonancia é a que se evita coa escala temperada moderna, e que é a que estamos afeitos a escoitar.
Pero, realmente usaban 7 oitavas os gregos? Pois non, a verdade. Nin María Callas, vaia. Deixádeme que vos explique todo isto das quintas doutro xeito, a ver se así.
Rebobinemos un pouco ata o punto onde vos comentaba que un intervalo de cuarta non era máis ca un de quinta “marcha atrás”: se subimos un intervalo de quinta e logo reducimos unha oitava, o que estamos a facer é baixar un intervalo de cuarta.
— Estás a tomarme o pelo?
Que non, que non, xa o expliquei antes. Imos velo de novo:
- Subir unha quinta é multiplica-la frecuencia orixinal por unha razón de 3:2.
- Baixar unha oitava é dividi-la frecuencia por 2.
- Se subimos unha quinta e baixamos unha oitava, o factor que estamos a aplicar é de (3/2)/2 = 3/4.
- Multiplicar por 3/4 é o mesmo ca dividir por 4/3.
- 4/3 é a proporción dun intervalo de cuarta, e se estamos a dividir é que estamos baixando en lugar de subir.
- De todo isto podemos asegurar que subir unha quinta e logo baixar unha oitava equivale en conxunto a baixar unha cuarta.
- Entendedes agora o da quinta “marcha atrás”?
Pois imos construír a progresión de quintas, pero sen que se nos disparen as oitavas. Non imos ir subindo quinta tras quinta, senón que imos ir aplicando unha subida de quinta, logo unha baixada de cuarta, despois subimos outra quinta, a continuación baixamos outra cuarta, e así sucesivamente. Quedaróanos isto:
| Intervalo | Frecuencia de partida | Relación | Frecuencia da quinta |
|---|---|---|---|
| Tónica | 440 Hz | 1:1 | 440 Hz |
| ↑ Quinta | 440 Hz | 3:2 | 660 Hz |
| ↓ Cuarta | 660 Hz | 3:4 | 495 Hz |
| ↑ Quinta | 495 Hz | 3:2 | 742,5 Hz |
| ↓ Cuarta | 742,5 Hz | 3:4 | 556,875 Hz |
| ↑ Quinta | 835,3125 Hz | 3:2 | 835,3125 Hz |
| ↓ Cuarta | 626,484375 Hz | 3:4 | 626,484375 Hz |
| ↑ Quinta | 939,7265625 Hz | 3:2 | 939,7265625 Hz |
| ↓ Cuarta | 704,794921875 Hz | 3:4 | 704,794921875 Hz |
| ↑ Quinta | 1057,192382812 Hz | 3:2 | 1057,192382812 Hz |
| ↓ Cuarta | 792,894287109 Hz | 3:4 | 792,894287109 Hz |
| ↑ Quinta | 1189,341430664 Hz | 3:2 | 1189,341430664 Hz |
| ↓ Cuarta | 892,006072998 Hz | 3:4 | 892,006072998 Hz |
Estos son os sons correspondentes:
Veredes que con este sistema de xeración de quintas non se nos disparan as frecuencias tanto coma antes. Pero aínda así, hai algunhas que sobrepasaron a oitava (se a nosa tónica é de 440 Hz, todo o que esté de 880 Hz para arriba estará noutra oitava diferente). Imos normalizalo todo, outra vez, para deixalo todo dentro da mesma oitava:
| Intervalo | Frecuencia sen corrixir | Corrección | Frecuencia corrixida |
|---|---|---|---|
| Tónica | 440 Hz | Non | 440 Hz |
| ↑ Quinta | 660 Hz | Non | 660 Hz |
| ↓ Cuarta | 495 Hz | Non | 495 Hz |
| ↑ Quinta | 742,5 Hz | Non | 742,5 Hz |
| ↓ Cuarta | 556,875 Hz | Non | 556,875 Hz |
| ↑ Quinta | 835,3125 Hz | Non | 835,3125 Hz |
| ↓ Cuarta | 626,484375 Hz | Non | 626,484375 Hz |
| ↑ Quinta | 939,7265625 Hz | :2 | 469,86328125 Hz |
| ↓ Cuarta | 704,794921875 Hz | Non | 704,794921875 Hz |
| ↑ Quinta | 1057,192382812 Hz | :2 | 528,596191406 Hz |
| ↓ Cuarta | 792,894287109 Hz | Non | 792,894287109 Hz |
| ↑ Quinta | 1189,341430664 Hz | :2 | 594,670715332 Hz |
| ↓ Cuarta | 892,006072998 Hz | Non | 446,003036499 Hz |
Vaia! Saíunos exactamente o mesmo que cando só subíamos quintas! Pois claro que sí, xa o demostramos antes. E igual ca no cálculo anterior, acabamos cun valor que é moi próximo á frecuencia inicial, pero non exactamente igual: a quinta do lobo.
Estes serían os sons correspondentes xa coas frecuencias corrixidas:
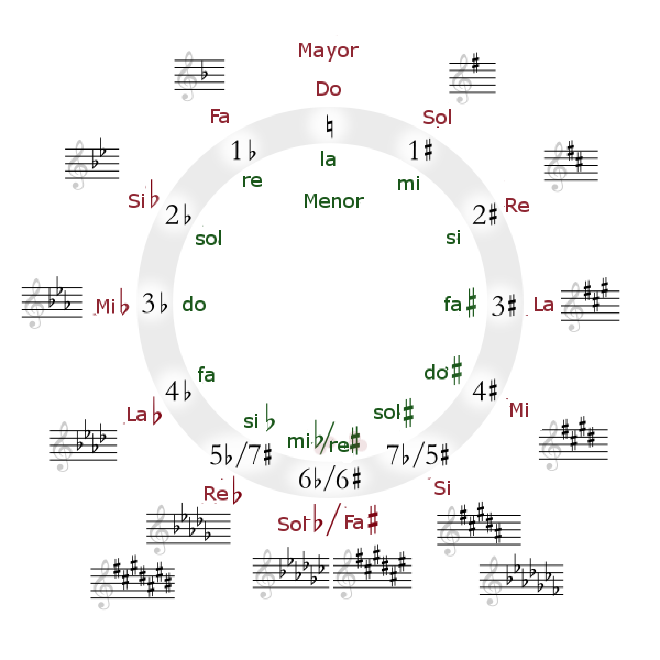
Esta progresión de quintas ou, mellor dito, de quintas ascendentes e cuartas descendentes, podémola ver nas partituras musicais ao comezo dun pentagrama, no que se coñece como armadura:
Como podedes ver, as armaduras con díeses (os símbolos con forma de cancelo) seguen a progresión Fa-Do-Sol-Re-La-Mi-Si. Nas que levan bemoles, a progresión é a inversa: Si-Mi-La-Re-Sol-Do-Fa. E nos dous casos son progresións de quintas.
Se tomamos calquera nota base, e aplicamos esa secuencia de quintas/cuartas, o que obtemos son as 12 notas dunha escala cromática. Para entendérmonos, a escala cromática contén todas as notas da escala musical que xa coñecemos todos (a escala diatónica que construímos antes), xunto cos sostidos/bemoles dos tonos intermedios (7 notas naturais da escala diatónica máis 5 notas alteradas). No teclado dun piano, a escala diatónica de Do estaría formada polas teclas brancas, mentres que a escala cromática de Do estaría formada por tódalas teclas, brancas e negras.
A secuencia de quintas, ordenada nun círculo, é coñecida como Círculo de Quintas, mundialmente famoso entre os guitarristas principalmente:
Veña, que estamos xa case rematando. Imos reordenar as notas anteriores de máis graves a máis agudas, e vexamos o que temos. Para rematar ben a oitava, puxemos ó final a nota de 892 (e pico) Hz sin corrixirlle a frecuencia, para que nos quede unha oitava máis alta e pechar ben a escala:
| Posición | Frecuencia sen corrixir | Frecuencia corrixida |
|---|---|---|
| 1 | 440 Hz | 440 Hz |
| 2 | 939,7265625 Hz | 469,86328125 Hz |
| 3 | 495 Hz | 495 Hz |
| 4 | 1057,192382812 Hz | 528,596191406 Hz |
| 5 | 556,875 Hz | 556,875 Hz |
| 6 | 1189,341430664 Hz | 594,670715332 Hz |
| 7 | 626,484375 Hz | 626,484375 Hz |
| 8 | 660 Hz | 660 Hz |
| 9 | 704,794921875 Hz | 704,794921875 Hz |
| 10 | 742,5 Hz | 742,5 Hz |
| 11 | 792,894287109 Hz | 792,894287109 Hz |
| 12 | 835,3125 Hz | 835,3125 Hz |
| 13 | 892,006072998 Hz | 892,006072998 Hz |
E aquí os sons:
Que tal? Soa decente, non? Se todavía non vos di nada a secuencia anterior, probade a reproducir-los sons das posicións 1-3-5-6-8-10-12-13, que corresponderían coa escala diatónica. Agora si?
Pois noraboa. Só cunhas matemáticas básicas acabamos de construír unha escala cromática.
Para os que vos estades a preguntar se a afinación pitagórica mellora algo respecto da natural, aquí tedes a comparación dos intervalos:
| Nota ou grado | Proporción do intervalo coa nota anterior na afinación natural |
Proporción do intervalo coa nota anterior na afinación pitagórica |
|---|---|---|
| 1º | 1/1 | 1/1 |
| 2º | 9/8 | (3/2)·(3/4) = 9/8 |
| 3º | 10/9 | (3/2)·(3/4) = 9/8 |
| 4º | 16/15 | (3/2)4·(3/4)3·(1/2) = 2187/2048 |
| 5º | 9/8 | 2·(4/3)5·(2/3)5 = 131072/177147 |
| 6º | 9/8 | (3/2)·(3/4) = 9/8 |
| 7º | 10/9 | (3/2)·(3/4) = 9/8 |
| 1º (Oitava) | 16/15 | (4/3)2·(2/3)3 = 128/243 |
Para non estendernos moito, déixovos a vós que fagades os cálculos. Tan só tedes que ir revisando cales son os factores polos que temos que multiplicar a frecuencia fundamental para ir chegando a cada unha das notas. Tedes que ter en conta que as notas da escala cromática que se corresponden coa escala diatónica son as posicións 1-3-5-6-8-10-12-13 que dixemos antes.
O que si podemos dicir é que a afinación pitagórica é un chisco máis homoxénea cá afinación natural, porque na natural tan só tiñamos tres intervalos con proporción 9/8 e na pitagórica temos catro.
— Menos mal, vaia chapa. Costoume quedar calado e non mandar todo a tomar vento. Xa rematamos, non?
— Mmmmm, non.
— ¿Non?
— Non.
— (xura en varias linguas mortas)
Esa pequena distancia lobuna… #
Temos un pequeno problemiña coa quinta do lobo. Imos escoitar de novo a primeira nota da secuencia anterior, a tónica, xunto coa posición 13 que é a mesma nota, pero na seguinte oitava:
Se tedes un oído medio normal, soaríavos medio ben. Se tedes un oído algo fino, veríades que “rechía” un pouco.
Imos escoitar agora a mesma nota, pero coa súa oitava natural, isto é, a oitava que sae ó duplicar a frecuencia:
Escoitade varias veces ambo-los dous sons, e remataredes apreciando a (non tan) sutil diferenza. Se despois de varias escoitas alternando os dous sons seguides sen apreciar a diferenza, que saibades que Mike Oldfield está moi preocupado pola vosa saúde. URL
O son coa oitava pitagórica amosa unha lixeira disonancia, e explícase porque a frecuencia da oitava non é exactamente o dobre da frecuencia base. No caso da oitava natural, non existe disonancia porque unha frecuencia é exactamente o dobre da outra.
A única alternativa para asegurar que as oitavas se manteñen, é facer que os intervalos dentro da escala cromática non sexan todos iguais.
Imos, Marty. Temos que viaxar uns cantos séculos cara o futuro. #
Ao longo do tempo probáronse sistemas para cadrar a afinación e evita-la quinta do lobo, pero as Matemáticas son testudas e é inevitable que algún dos intervalos quede desigualado se queremos manter as oitavas naturais. Das diferentes posibilidades en canto a decidir onde se poñían as desigualdades entre os semitonos xurdiron diferentes sistemas de afinación, como por exemplo a afinación mesotónica baseada en terceiras maiores.
Era un problema isto de ter semitóns desiguais? Pois si e non. Musicalmente non era demasiado grave, é dicir, non soaba mal. Pero tiña inconvintes, por exemplo, se tentabas tocar con instrumentos construídos para diferentes oitavas. Un instrumento construído para dar unha oitava natural de Do a Do non ía soar exactamente igual que si se construía para unha oitava natural de Mi a Mi. Ó tocar un Re en ambos instrumentos, soarían diferentes.
E chegamos ó século XVI.
A escala temperada. #
No século XVI os únicos que empregaban a afinación temperada eran os fabricantes de instrumentos de corda con trastes. Porén, os músicos de teclado todavía empregaban a afinación mesotónica e tardaron uns douscentos anos máis en adopta-la afinación temperada.
Atribúeselle a J. S. Bach a adopción da afinación temperada debido á súa obra O clave ben temperado, pero o certo é que nesta obra o bo de Johann só pretendía compoñer 24 preludios e 24 fugas que comprendesen tódalas tonalidades e non estaba pensando no temperamento igual senón no mesotónico, que era o que se levaba na súa época e máis ou menos quedaba resultón ó empregar diferentes tonalidades.
O sistema temperado non comezou a ser empregado polos grandes fabricantes de pianos ata xa entrado (e nalgúns casos, avanzado) o século XIX.
Pero que é iso do temperamento igual, afinación temperada, ou como queirades chamalo?
Pois non é máis ca unha resposta moi, moi simple, á pregunta: Podemos ter unha escala onde tódo-los semitóns sexan iguais?
Pois claro que sí. Vexamos como:
- O único que debemos ter en conta é que as oitavas deben serguir sendo naturais (a súa relación de frecuencias debe ser 2:1).
- Tódolos semitóns deben ser iguais, logo a relación de frecuencias entre unha nota e a seguinte debe ser sempre a mesma.
- Partindo da nota que lle chamaremos tónica, ó dar doce saltos debemos chegar á súa oitava natural.
- Polo tanto, se a frecuencia da tónica é Ft e a relación do intervalo é i, temos que Ft·i·i … ·i (12 veces) = 2·Ft
- Se escribimos eso mesmo empregando potencias, temos que Ft·i12 = 2·Ft
- E polo tanto a relación de frecuencias que estamos a procurar é a raíz décimo segunda de 2, que equivale a un factor de 1,059463094359.
— Pero a raíz décimo segunda de 12 non é un número enteiro, non?
— Non.
— E tampouco é unha fracción de números enteiros, non si?
— Non.
— E que opinan os gregos de todo isto?
— Pitágoras xa fai moito que morreu, o pobre.
— Pois menos mal. Se ve isto morría outra vez, do susto.
Pois si. O mundo occidental tardou moitos séculos en tira-la toalla e olvidarse dos número enteiros para construír escalas. A afinación temperada acabou por impoñerse e é a que se emprega na actualidade. Os nosos oídos afixéronse e xa non nos resulta estraño que nun intervalo de quinta a relación de frecuencias xa no sexa exactamente 3:2, senón algo lixeiramente diferente.
Cales serían as frecuencias da nosa escala coa afinación temperada? Pois se partimos da mesma nota base, isto é, un La4 a 440 Hz, teríamos isto:
| Nota | Frecuencia |
|---|---|
| La4 | 440 Hz |
| La#4 | 466,1637615181 Hz |
| Si4 | 493,8833012561 Hz |
| Do5 | 523,2511306012 Hz |
| Do#5 | 554,3652619537 Hz |
| Re5 | 587,3295358348 Hz |
| Re#5 | 622,2539674442 Hz |
| Mi5 | 659,2551138257 Hz |
| Fa5 | 698,4564628660 Hz |
| Fa#5 | 739,9888454233 Hz |
| Sol5 | 783,9908719635 Hz |
| Sol#5 | 830,6093951599 Hz |
| La5 | 880 Hz |
E estes serían os sons:
É moi diferente a escala temperada? #
Cal é a relación de frecuencias nun intervalo de quinta coa afinación temperada? Pois se collemo-las frecuencias da nota tónica e da oitava nota (estamos nunha escala cromática, e o quinto grado da escala diatónica corresponde coa oitava nota da escala cromática) temos que:
659,2551138257 / 440 = 1,498307076877
, que é moi semellante á relación de 3:2 da quinta natural, pero non é exactamente igual. Sentímolo moito, Pitágoras.
Vexamos como de diferente é a afinación temperada respecto da pitagórica:
| Nota | Frecuencia pitagórica | Frecuencia temperada | Diferenza |
|---|---|---|---|
| La4 | 440 Hz | 440 Hz | 0 % |
| La#4 | 469,86328125 Hz | 466,1637615181 Hz | −0,787361 % |
| Si4 | 495 Hz | 493,8833012561 Hz | −0,225596 % |
| Do4 | 528,596191406 Hz | 523,2511306012 Hz | −1,011180 % |
| Do#4 | 556,875 Hz | 554,3652619537 Hz | −0,450682 % |
| Re5 | 594,670715332 Hz | 587,3295358348 Hz | −1,234495 % |
| Re#5 | 626,484375 Hz | 622,2539674442 Hz | −0,675261 % |
| Mi5 | 660 Hz | 659,2551138257 Hz | −0,112862 % |
| Fa5 | 704,794921875 Hz | 698,4564628660 Hz | −0,899334 % |
| Fa#5 | 742,5 Hz | 739,9888454233 Hz | −0,338203 % |
| Sol5 | 792,894287109 Hz | 783,9908719635 Hz | −1,122901 % |
| Sol#5 | 835,3125 Hz | 830,6093951599 Hz | −0,563035 % |
| La5 | 880 Hz | 880 Hz | 0 % |
Podemos apreciar que a escala temperada ten o seu mínimo de separación precisamente no intervalo de quinta (a oitava nota da escala cromática). No resto de grados a desviación é maior, pero só en tres casos supera o 1% de desviación.
A pesar destas desviacións da escala temperada, posúe a gran vantaxe de que podemos coller calquera frecuencia base e a partir dela calcular tódalas notas da súa escala cromática con tan só multiplicar pola raíz décimo segunda de 2. Cando cheguemos á oitava, coincidirá coa oitava natural.
As notas terán sempre a mesma frecuencia, sexa cal sexa a tonalidade que estemos empregando. Isto quere dicir que un Re4 terá sempre a mesma frecuencia tanto se partimos dun Do4 como tónica, coma se partimos dun Mi3. Cando cheguemos ó Re4, a frecuencia será a mesma nos dous casos, e por iso os instrumentos que empregan a afinación temperada non están suxeitos a unha tonalidade en concreto, senón que traballan ben en calquera delas.
Xa, por último, imos escoita-las diferenzas entre os intervalos naturais e os temperados.
Aquí tedes un intervalo de quinta natural e outro de quinta temperada:
Aquí unha terceira natural e unha terceira temperada:
E para rematar, imos combinar unha terceira e unha quinta formando un acorde de La Maior natural, e o mesmo acorde de La Maior, pero temperado:
A que custa distinguilos? Cando comparábamos a oitava natural coa oitava pitagórica, a diferenza entre amba-las dúas notas era de algo máis do 1,3%. Podíase distinguir entre ambos a pouco que nos fixásemos. No caso destes acordes temperados respecto dos naturais, as diferenzas son de un 0,45% para o intervalo de terceira e un 0,11% para o intervalo de quinta. Hai que ter xa certo oído para distinguilos. Eu, persoalmente, non son quen.
Parece que o da afinación temperada non é un mal invento.